K Sum Paths

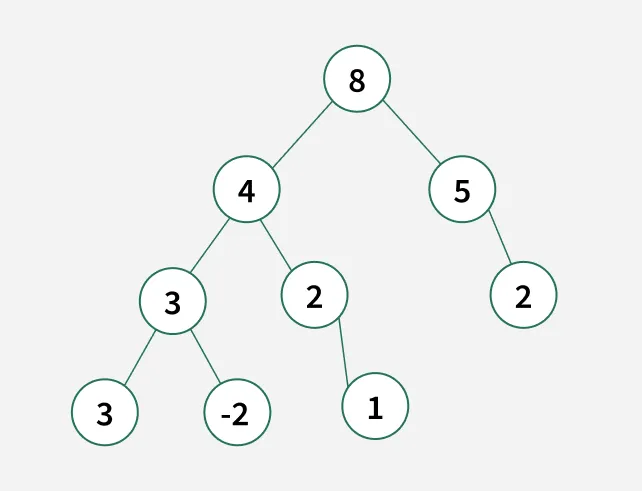
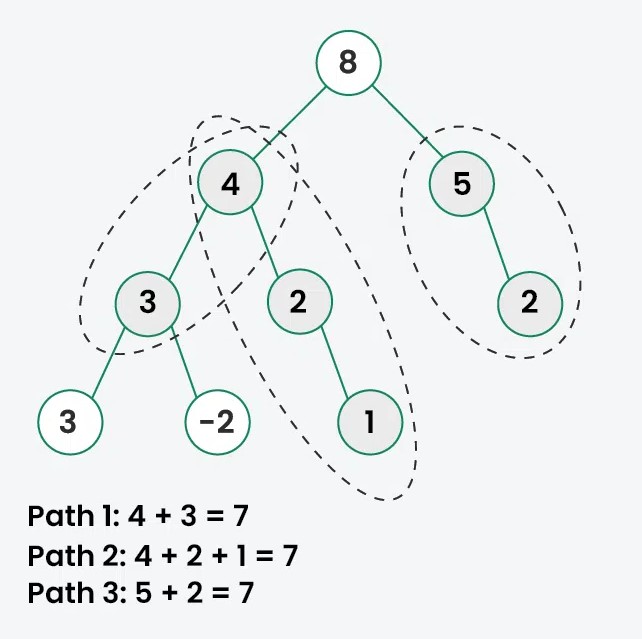
Given a binary tree and an integer k, determine the number of downward-only paths where the sum of the node values in the path equals k. A path can start and end at any node within the tree but must always move downward (from parent to child).

Examples:

Input: k = 7 

Output: 3
Explanation: The following paths sum to k 

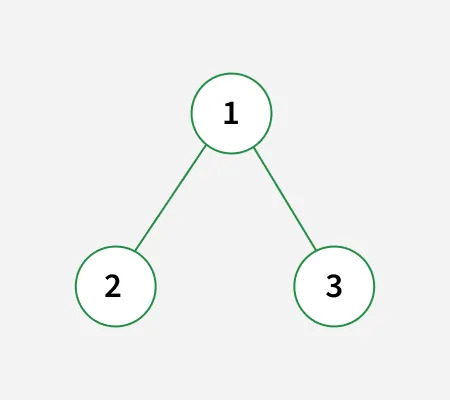
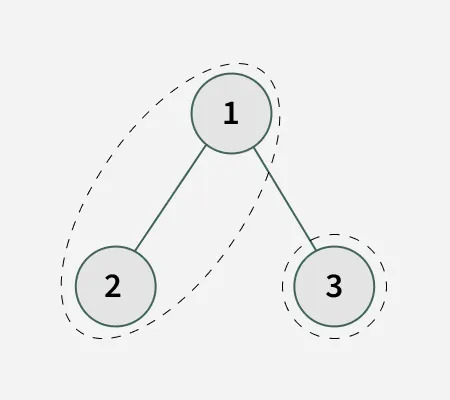
Input: k = 3

Output: 2
Explanation:
Path 1 : 1 -> 2 (Sum = 3)
Path 2 : 3 (Sum = 3)

Constraints:

• 1 ≤ number of nodes ≤ 10⁴
• -100 ≤ node value ≤ 100
• -10⁹ ≤ k ≤ 10⁹

Approach 01:

#include <unordered_map>
using namespace std;

class Solution {
  public:
    void solve(Node* node, int currentSum, int targetSum, unordered_map<int, int> &prefixSumMap, int &pathCount) {
        if (!node)
            return;
        
        currentSum += node->data;
        
        if (currentSum == targetSum)
            pathCount++;
        
        pathCount += prefixSumMap[currentSum - targetSum];
        
        prefixSumMap[currentSum]++;
        
        solve(node->left, currentSum, targetSum, prefixSumMap, pathCount);
        solve(node->right, currentSum, targetSum, prefixSumMap, pathCount);
        
        prefixSumMap[currentSum]--;  // Backtrack
    }

    int sumK(Node* root, int targetSum) {
        int pathCount = 0;
        unordered_map<int, int> prefixSumMap;
        solve(root, 0, targetSum, prefixSumMap, pathCount);
        return pathCount;
    }
};

from collections import defaultdict

class Solution:
    def solve(self, node, currentSum, targetSum, prefixSumMap, pathCount):
        if not node:
            return
        
        currentSum += node.data
        
        if currentSum == targetSum:
            pathCount[0] += 1
        
        pathCount[0] += prefixSumMap[currentSum - targetSum]
        
        prefixSumMap[currentSum] += 1
        
        self.solve(node.left, currentSum, targetSum, prefixSumMap, pathCount)
        self.solve(node.right, currentSum, targetSum, prefixSumMap, pathCount)
        
        prefixSumMap[currentSum] -= 1  

    def sumK(self, root, targetSum):
        pathCount = [0]  
        prefixSumMap = defaultdict(int)
        self.solve(root, 0, targetSum, prefixSumMap, pathCount)
        return pathCount[0]

Time Complexity:

• Tree Traversal:

  Each node is visited once, leading to a complexity of \( O(N) \), where \( N \) is the number of nodes in the tree.

• Prefix Sum Operations:

  Each node performs constant-time operations (\( O(1) \)) involving the prefix sum map.

• Overall Time Complexity:

  \( O(N) \), since each node is processed in constant time.

Space Complexity:

• Recursive Stack:

  In the worst case (skewed tree), the recursion depth is \( O(N) \), while in a balanced tree, it is \( O(\log N) \).

• Prefix Sum Map:

  In the worst case, the map stores a sum for each node, taking \( O(N) \) space.

• Overall Space Complexity:

  Worst case: \( O(N) \), Best case (balanced tree): \( O(\log N) \).