You are given a 2D integer grid of size m x n and an integer x. In one operation, you can add x to or subtract x from any element in the grid.
A uni-value grid is a grid where all the elements of it are equal.
Return the minimum number of operations to make the grid uni-value. If it is not possible, return -1.
Example 1:
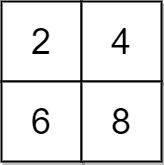
Input: grid = [[2,4],[6,8]], x = 2 Output: 4 Explanation: We can make every element equal to 4 by doing the following: - Add x to 2 once. - Subtract x from 6 once. - Subtract x from 8 twice. A total of 4 operations were used.
Example 2:
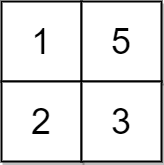
Input: grid = [[1,5],[2,3]], x = 1 Output: 5 Explanation: We can make every element equal to 3.
Example 3:
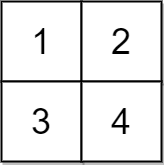
Input: grid = [[1,2],[3,4]], x = 2 Output: -1 Explanation: It is impossible to make every element equal.
Constraints:
m == grid.lengthn == grid[i].length1 <= m, n <= 1051 <= m * n <= 1051 <= x, grid[i][j] <= 104
Approach 01:
-
C++
-
Python
#include <vector>
#include <algorithm>
using namespace std;
class Solution {
public:
int minOperations(vector<vector<int>>& grid, int stepSize) {
vector<int> flattenedGrid;
for (const vector<int>& row : grid) {
flattenedGrid.insert(flattenedGrid.end(), row.begin(), row.end());
}
if (ranges::any_of(flattenedGrid, [&](int value) { return (value - flattenedGrid[0]) % stepSize; })) {
return -1;
}
int totalOperations = 0;
nth_element(flattenedGrid.begin(),
flattenedGrid.begin() + flattenedGrid.size() / 2,
flattenedGrid.end());
int medianValue = flattenedGrid[flattenedGrid.size() / 2];
for (const int value : flattenedGrid) {
totalOperations += abs(value - medianValue) / stepSize;
}
return totalOperations;
}
};
Time Complexity:
- Flattening the Grid:Inserting all elements from a 2D grid into a 1D vector takes \( O(mn) \), where \( m \) is the number of rows and \( n \) is the number of columns.
- Divisibility Check:Checking if all values have the same remainder when divided by
stepSizetakes \( O(mn) \). - Finding the Median:Using
nth_elementto find the median in an unordered array takes \( O(mn) \) on average. - Computing Operations:Iterating through the array to compute the total operations takes \( O(mn) \).
- Total Time Complexity:The overall time complexity is \( O(mn) \).
Space Complexity:
- Flattened Grid Storage:Storing all elements of the grid in a 1D list takes \( O(mn) \) space.
- Additional Variables:Only a few additional variables are used, taking \( O(1) \) extra space.
- Total Space Complexity:The overall space complexity is \( O(mn) \).
from typing import List
class Solution:
def minOperations(self, grid: List[List[int]], stepSize: int) -> int:
flattenedGrid = [value for row in grid for value in row]
if any((value - flattenedGrid[0]) % stepSize for value in flattenedGrid):
return -1
totalOperations = 0
flattenedGrid.sort()
medianValue = flattenedGrid[len(flattenedGrid) // 2]
for value in flattenedGrid:
totalOperations += abs(value - medianValue) // stepSize
return totalOperations
Time Complexity:
- Flattening the Grid:
Flattening the 2D grid into a 1D list takes \( O(mn) \), where \( m \) is the number of rows and \( n \) is the number of columns.
- Divisibility Check:
Checking if all values have the same remainder when divided by
stepSizetakes \( O(mn) \). - Sorting:
Sorting the flattened array takes \( O(mn \log(mn)) \).
- Computing Operations:
Iterating through the sorted array to compute the total operations takes \( O(mn) \).
- Total Time Complexity:
The overall time complexity is \( O(mn \log(mn)) \).
Space Complexity:
- Flattened Grid Storage:
Storing all elements of the grid in a 1D list takes \( O(mn) \) space.
- Additional Variables:
Only a few additional variables are used, taking \( O(1) \) extra space.
- Total Space Complexity:
The overall space complexity is \( O(mn) \).