DFS of Graph

Given a connected undirected graph represented by a 2-d adjacency list adj[][], where each adj[i] represents the list of vertices connected to vertex i. Perform a Depth First Search (DFS) traversal starting from vertex 0, visiting vertices from left to right as per the given adjacency list, and return a list containing the DFS traversal of the graph.

Note: Do traverse in the same order as they are in the given adjacency list.

Examples:

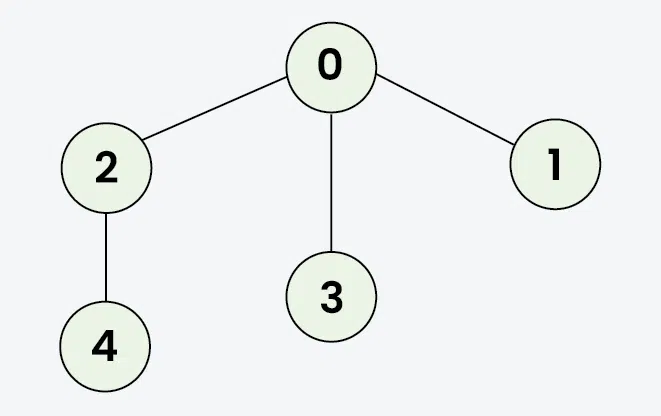
Input: adj[][] = [[2, 3, 1], [0], [0, 4], [0], [2]]

Output: [0, 2, 4, 3, 1]
Explanation: Starting from 0, the DFS traversal proceeds as follows:
Visit 0 → Output: 0 
Visit 2 (the first neighbor of 0) → Output: 0, 2 
Visit 4 (the first neighbor of 2) → Output: 0, 2, 4 
Backtrack to 2, then backtrack to 0, and visit 3 → Output: 0, 2, 4, 3 
Finally, backtrack to 0 and visit 1 → Final Output: 0, 2, 4, 3, 1

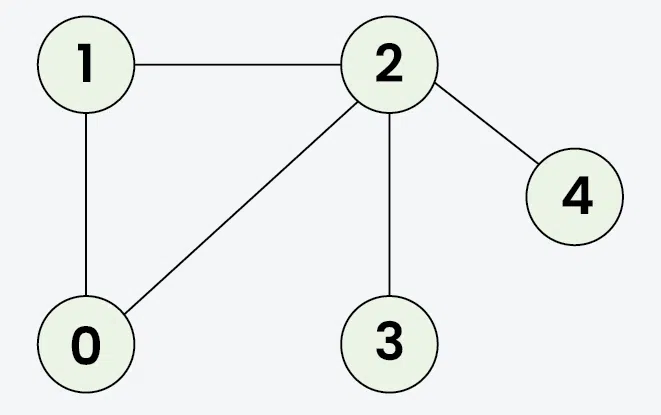
Input: adj[][] = [[1, 2], [0, 2], [0, 1, 3, 4], [2], [2]]

Output: [0, 1, 2, 3, 4]
Explanation: Starting from 0, the DFS traversal proceeds as follows: 
Visit 0 → Output: 0 
Visit 1 (the first neighbor of 0) → Output: 0, 1 
Visit 2 (the first neighbor of 1) → Output: 0, 1, 2 
Visit 3 (the first neighbor of 2) → Output: 0, 1, 2, 3 
Backtrack to 2 and visit 4 → Final Output: 0, 1, 2, 3, 4

Constraints:
1 ≤ adj.size() ≤ 10⁴
1 ≤ adj[i][j] ≤ 10⁴

Approach 01:

#include <vector>

using namespace std;

class Solution {
public:
    void dfsHelper(int node, vector<vector<int>>& adjacencyList, vector<int>& visited, vector<int>& traversalResult) {
        visited[node] = 1;  
        traversalResult.push_back(node); 

        for (auto& neighbor : adjacencyList[node]) {
            if (!visited[neighbor]) {  
                dfsHelper(neighbor, adjacencyList, visited, traversalResult);
            }
        }
    }
    
    vector<int> dfs(vector<vector<int>>& adjacencyList) {
        int numVertices = adjacencyList.size();
        vector<int> visited(numVertices, 0);
        vector<int> traversalResult;
        
        int startNode = 0;  
        dfsHelper(startNode, adjacencyList, visited, traversalResult);
        
        return traversalResult; 
    }
};

from typing import List

class Solution:
    def dfsHelper(self, node: int, adjacencyList: List[List[int]], visited: List[bool], traversalResult: List[int]) -> None:
        visited[node] = True  
        traversalResult.append(node)  
        
        for neighbor in adjacencyList[node]:
            if not visited[neighbor]:  
                self.dfsHelper(neighbor, adjacencyList, visited, traversalResult)
                
    def dfs(self, adjacencyList: List[List[int]]) -> List[int]:
        numVertices = len(adjacencyList)
        visited = [False] * numVertices  
        traversalResult = []  
        startNode = 0  
        
        self.dfsHelper(startNode, adjacencyList, visited, traversalResult)
        
        return traversalResult

Time Complexity:

• Depth-First Search Traversal:

  Each vertex is visited once, and each edge is explored once, leading to a total complexity of \( O(V + E) \), where \( V \) is the number of vertices and \( E \) is the number of edges.

• Recursive Calls:

  Each recursive call processes one vertex and explores its neighbors, but since each edge is traversed once, the recursion itself remains within \( O(V + E) \).

• Total Time Complexity:

  The overall time complexity is \( O(V + E) \).

Space Complexity:

• Visited Array:

  The visited array stores information for each vertex, consuming \( O(V) \) space.

• Traversal Result:

  The traversalResult stores all visited nodes, requiring \( O(V) \) space.

• Recursive Stack:

  In the worst case (a linear graph), the recursive stack depth reaches \( O(V) \).

• Total Space Complexity:

  Since all dominant terms are \( O(V) \), the overall space complexity is \( O(V) \).