1552. Magnetic Force Between Two Balls

In the universe Earth C-137, Rick discovered a special form of magnetic force between two balls if they are put in his new invented basket. Rick has n empty baskets, the ith basket is at position[i], Morty has m balls and needs to distribute the balls into the baskets such that the minimum magnetic force between any two balls is maximum.

Rick stated that magnetic force between two different balls at positions x and y is |x - y|.

Given the integer array position and the integer m. Return the required force.

Example 1:

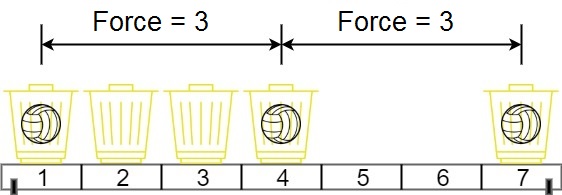
Input: position = [1,2,3,4,7], m = 3
Output: 3
Explanation: Distributing the 3 balls into baskets 1, 4 and 7 will make the magnetic force between ball pairs [3, 3, 6]. The minimum magnetic force is 3. We cannot achieve a larger minimum magnetic force than 3.

Example 2:

Input: position = [5,4,3,2,1,1000000000], m = 2
Output: 999999999
Explanation: We can use baskets 1 and 1000000000.

Constraints:

• n == position.length
• 2 <= n <= 105
• 1 <= position[i] <= 109
• All integers in position are distinct.
• 2 <= m <= position.length

Approach 01:

#include <algorithm>
#include <ranges>
#include <vector>

class Solution {
public:
    int maxDistance(std::vector<int>& position, int m) {
        std::ranges::sort(position);

        int left = 1;
        int right = position.back() - position.front();

        while (left < right) {
            const int mid = right - (right - left) / 2;
            if (numBalls(position, mid) >= m) // There're too many balls.
                left = mid;
            else // There're too few balls.
                right = mid - 1;
        }

        return left;
    }

private:
    int numBalls(const std::vector<int>& position, int force) {
        int balls = 0;
        int prev_position = -force;
        for (const int pos : position)
            if (pos - prev_position >= force) {
                ++balls;
                prev_position = pos;
            }
        return balls;
    }
};

from typing import List

class Solution:
    def maxDistance(self, position: List[int], m: int) -> int:
        position.sort()

        left = 1
        right = position[-1] - position[0]

        while left < right:
            mid = right - (right - left) // 2
            if self.num_balls(position, mid) >= m:  # There're too many balls.
                left = mid
            else:  # There're too few balls.
                right = mid - 1

        return left

    def num_balls(self, position: List[int], force: int) -> int:
        balls = 0
        prev_position = -force
        for pos in position:
            if pos - prev_position >= force:
                balls += 1
                prev_position = pos
        return balls

Time Complexity

1. Sorting: The first step is to sort the position array, which takes \(O(n \log n)\), where \(n\) is the number of elements in the position array.

2. Binary Search: The binary search operates over the range of possible forces, which has a size proportional to the difference between the maximum and minimum elements in position, \(O(\max(\text{position}) – \min(\text{position}))\).

3. Num Balls Calculation: For each mid value in the binary search, the num_balls function iterates through the position array, which takes \(O(n)\) time.

Combining these:

The binary search will take \(O(\log(\max(\text{position}) – \min(\text{position})))\) iterations.

In each iteration, the num_balls function is called, which takes \(O(n)\) time.

Therefore, the total time complexity is:
\(
O(n \log n) + O(\log(\max(\text{position}) – \min(\text{position})) \cdot n)
\)
Since the sorting term \(O(n \log n)\) is generally dominated by the binary search term for large \(n\), the overall time complexity is:
\(
O(n \log n + n \log(\max(\text{position}) – \min(\text{position})))
\)

Space Complexity

1. Sorting: Sorting typically takes \(O(n)\) additional space for the sort operation.

2. Binary Search and Num Balls Calculation: The binary search and num_balls function use a constant amount of additional space, \(O(1)\).

Therefore, the overall space complexity is: \(O(n)\)