There are n friends that are playing a game. The friends are sitting in a circle and are numbered from 1 to n in clockwise order. More formally, moving clockwise from the ith friend brings you to the (i+1)th friend for 1 <= i < n, and moving clockwise from the nth friend brings you to the 1st friend.
The rules of the game are as follows:
- Start at the
1stfriend. - Count the next
kfriends in the clockwise direction including the friend you started at. The counting wraps around the circle and may count some friends more than once. - The last friend you counted leaves the circle and loses the game.
- If there is still more than one friend in the circle, go back to step
2starting from the friend immediately clockwise of the friend who just lost and repeat. - Else, the last friend in the circle wins the game.
Given the number of friends, n, and an integer k, return the winner of the game.
Example 1:
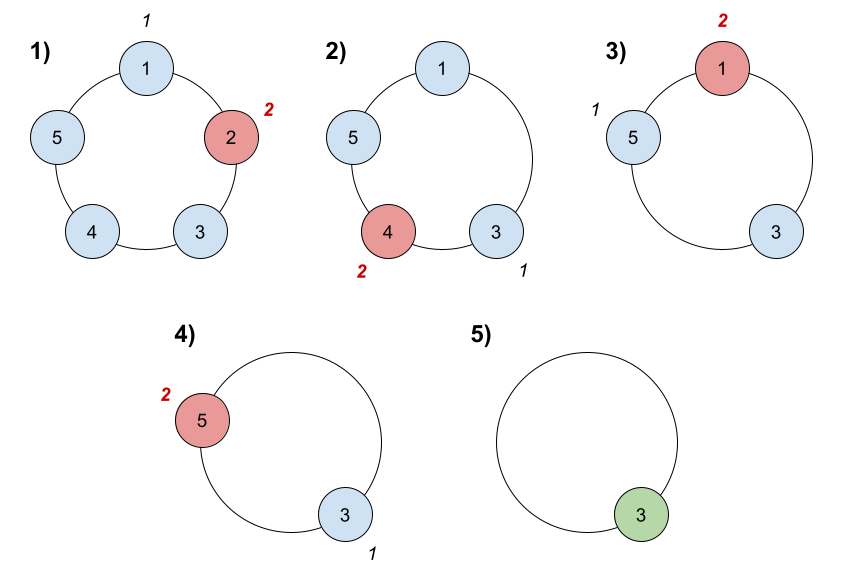
Input: n = 5, k = 2 Output: 3 Explanation: Here are the steps of the game: 1) Start at friend 1. 2) Count 2 friends clockwise, which are friends 1 and 2. 3) Friend 2 leaves the circle. Next start is friend 3. 4) Count 2 friends clockwise, which are friends 3 and 4. 5) Friend 4 leaves the circle. Next start is friend 5. 6) Count 2 friends clockwise, which are friends 5 and 1. 7) Friend 1 leaves the circle. Next start is friend 3. 8) Count 2 friends clockwise, which are friends 3 and 5. 9) Friend 5 leaves the circle. Only friend 3 is left, so they are the winner.
Example 2:
Input: n = 6, k = 5 Output: 1 Explanation: The friends leave in this order: 5, 4, 6, 2, 3. The winner is friend 1.
Constraints:
1 <= k <= n <= 500
Approach 01:
-
C++
-
Python
class Solution {
public:
int findTheWinner(int n, int k) {
vector<bool> friends(n);
int friend_count = n;
int fp = 0;
while (friend_count > 1) {
for (int i = 0; i < k; ++i, ++fp)
while (friends[fp % n]){
++fp;
}
friends[(fp - 1) % n] = true;
--friend_count;
}
const auto it = find_if(friends.begin(), friends.end(), [](int f) { return !f; });
return distance(friends.begin(), it) + 1;
}
};
class Solution:
def findTheWinner(self, n: int, k: int) -> int:
friends = [False] * n
friend_count = n
fp = 0
while friend_count > 1:
for _ in range(k):
while friends[fp % n]:
fp += 1
fp += 1
friends[(fp - 1) % n] = True
friend_count -= 1
fp = 0
while friends[fp]:
fp += 1
return fp + 1
Time Complexity
-
Initialization:
Initializing the
friendsvector and variables takes \( O(n) \) time. -
While Loop:
The while loop runs until only one friend remains, so it executes \( O(n) \) times.
-
Inner For Loop:
Each iteration of the while loop involves a for loop that iterates
ktimes and a nested while loop that may iterate up to \( n \) times in the worst case. -
Overall Time Complexity:
The overall time complexity is \( O(n \cdot k \cdot n) = O(n^2 \cdot k) \).
Space Complexity
-
Space Usage:
The
friendsvector uses \( O(n) \) space to keep track of eliminated friends. -
Overall Space Complexity:
The overall space complexity is \( O(n) \).