Largest square formed in a matrix

Given a binary matrix mat of size n * m, find out the maximum length of a side of a square sub-matrix with all 1s.

Examples:

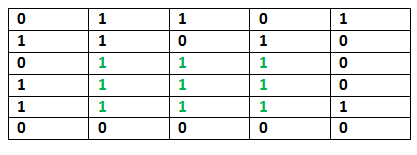
Input: n = 6, m = 5
mat = [[0, 1, 1, 0, 1], 
       [1, 1, 0, 1, 0],
       [0, 1, 1, 1, 0],
       [1, 1, 1, 1, 0],
       [1, 1, 1, 1, 1],
       [0, 0, 0, 0, 0]]
Output: 3
Explanation: 

The maximum length of a side of the square sub-matrix is 3 where every element is 1.

Input: n = 2, m = 2
mat = [[1, 1], 
       [1, 1]]
Output: 2
Explanation: The maximum length of a side of the square sub-matrix is 2. The matrix itself is the maximum sized sub-matrix in this case.

Input: n = 2, m = 2
mat = [[0, 0], 
       [0, 0]]
Output: 0
Explanation: There is no 1 in the matrix.

Expected Time Complexity: O(n*m)
Expected Auxiliary Space: O(n*m)

Constraints:
1 ≤ n, m ≤ 500
0 ≤ mat[i][j] ≤ 1 

Approach 01:

class Solution {
public:
    int maxSquare(int rows, int cols, vector<vector<int>> matrix) {
        int max_square_size = 0;
        
        for(int i = 0; i < rows; i++){
            for(int j = 0; j < cols; j++){
                if(matrix[i][j] == 1){
                    if(i == 0 || j == 0)
                        matrix[i][j] = 1;
                    else{
                        matrix[i][j] = min({matrix[i-1][j-1], matrix[i-1][j], matrix[i][j-1]}) + 1;
                    }
                    max_square_size = max(max_square_size, matrix[i][j]);
                }
            }
        }
        return max_square_size;
    }
};

from typing import List

class Solution:
    def maxSquare(self, rows: int, cols: int, matrix: List[List[int]]) -> int:
        max_square_size = 0
        
        for i in range(rows):
            for j in range(cols):
                if matrix[i][j] == 1:
                    if i == 0 or j == 0:
                        matrix[i][j] = 1
                    else:
                        matrix[i][j] = min(matrix[i-1][j-1], matrix[i-1][j], matrix[i][j-1]) + 1
                    max_square_size = max(max_square_size, matrix[i][j])
        
        return max_square_size

Time Complexity

• Nested Loops:

  The algorithm uses nested loops to traverse each element of the matrix. The outer loop runs \( \text{rows} \) times and the inner loop runs \( \text{cols} \) times.

• Overall Time Complexity:

  The overall time complexity is \( O(\text{rows} \times \text{cols}) \), where \( \text{rows} \) is the number of rows and \( \text{cols} \) is the number of columns in the matrix.

Space Complexity

• In-Place Modification:

  The algorithm modifies the input matrix in-place to store intermediate results. No additional space proportional to the size of the input is used.

• Overall Space Complexity:

  The overall space complexity is \( O(1) \), as the algorithm only uses a constant amount of extra space for variables such as max_square_size.