1105. Filling Bookcase Shelves

You are given an array books where books[i] = [thicknessi, heighti] indicates the thickness and height of the ith book. You are also given an integer shelfWidth.

We want to place these books in order onto bookcase shelves that have a total width shelfWidth.

We choose some of the books to place on this shelf such that the sum of their thickness is less than or equal to shelfWidth, then build another level of the shelf of the bookcase so that the total height of the bookcase has increased by the maximum height of the books we just put down. We repeat this process until there are no more books to place.

Note that at each step of the above process, the order of the books we place is the same order as the given sequence of books.

• For example, if we have an ordered list of 5 books, we might place the first and second book onto the first shelf, the third book on the second shelf, and the fourth and fifth book on the last shelf.

Return the minimum possible height that the total bookshelf can be after placing shelves in this manner.

Example 1:

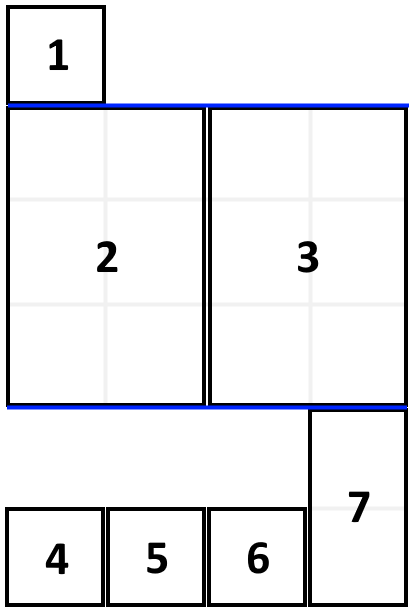
Input: books = [[1,1],[2,3],[2,3],[1,1],[1,1],[1,1],[1,2]], shelfWidth = 4
Output: 6
Explanation:
The sum of the heights of the 3 shelves is 1 + 3 + 2 = 6.
Notice that book number 2 does not have to be on the first shelf.

Example 2:

Input: books = [[1,3],[2,4],[3,2]], shelfWidth = 6
Output: 4

Constraints:

• 1 <= books.length <= 1000
• 1 <= thicknessi <= shelfWidth <= 1000
• 1 <= heighti <= 1000

Approach 01:

#include <bits/stdc++.h>

using namespace std;

class Solution {
public:
    int minHeightShelves(vector<vector<int>>& books, int shelfWidth) {
        // dp[i] represents the minimum height needed to place the first i books
        vector<int> dp(books.size() + 1, INT_MAX);
        dp[0] = 0;

        for (int i = 0; i < books.size(); ++i) {
            int currentShelfWidth = 0;
            int currentShelfHeight = 0;
            // Try placing books from index j to i on the current shelf.
            for (int j = i; j >= 0; --j) {
                const int bookWidth = books[j][0];
                const int bookHeight = books[j][1];
                currentShelfWidth += bookWidth;
                if (currentShelfWidth > shelfWidth)
                    break; // Shelf width exceeded, cannot place more books on this shelf.
                currentShelfHeight = max(currentShelfHeight, bookHeight);
                dp[i + 1] = min(dp[i + 1], dp[j] + currentShelfHeight);
            }
        }

        return dp.back();
    }
};

from typing import *

class Solution:
    def minHeightShelves(self, books: List[List[int]], shelfWidth: int) -> int:
        # dp[i] represents the minimum height needed to place the first i books
        dp = [float('inf')] * (len(books) + 1)
        dp[0] = 0

        for i in range(len(books)):
            currentShelfWidth = 0
            currentShelfHeight = 0
            # Try placing books from index j to i on the current shelf.
            for j in range(i, -1, -1):
                bookWidth = books[j][0]
                bookHeight = books[j][1]
                currentShelfWidth += bookWidth
                if currentShelfWidth > shelfWidth:
                    break  # Shelf width exceeded, cannot place more books on this shelf.
                currentShelfHeight = max(currentShelfHeight, bookHeight)
                dp[i + 1] = min(dp[i + 1], dp[j] + currentShelfHeight)

        return dp[-1]

Time Complexity

• Iterating Through Books:

  The outer loop iterates through each book once, which takes \( O(n) \) time, where \( n \) is the number of books.

• Placing Books on Shelves:

  The inner loop also iterates through the books but in reverse order, creating a nested loop that in total considers each pair of books, leading to \( O(n^2) \) time complexity for placing books on shelves.

• Overall Time Complexity:

  The overall time complexity is \( O(n^2) \), where \( n \) is the number of books.

Space Complexity

• Dynamic Programming Table:

  The dynamic programming table dp requires \( O(n) \) space, where \( n \) is the number of books.

• Overall Space Complexity:

  The overall space complexity is \( O(n) \), where \( n \) is the number of books.