Given the head of a singly linked list, the task is to rotate the linked list clockwise by k nodes, i.e., left-shift the linked list by k nodes, where k is a given positive integer smaller than or equal to length of the linked list.
Examples:
Input: linkedlist: 2->4->7->8->9 , k = 3 Output: 8->9->2->4->7 Explanation:
Rotate 1: 4 -> 7 -> 8 -> 9 -> 2 Rotate 2: 7 -> 8 -> 9 -> 2 -> 4 Rotate 3: 8 -> 9 -> 2 -> 4 -> 7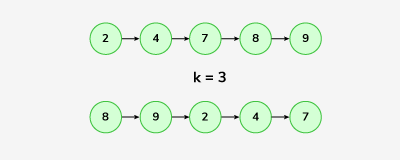
Input: linkedlist: 1->2->3->4->5->6->7->8 , k = 4 Output: 5->6->7->8->1->2->3->4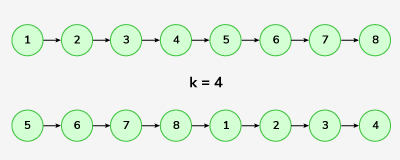
Expected Time Complexity: O(n)
Expected Auxiliary Space: O(1)
Constraints:
1 <= number of nodes <= 103
1 <= node -> data <= 104
1 <= k <= number of nodes
Approach 01:
-
C++
-
Python
class Solution {
public:
Node* rotate(Node* head, int k) {
Node* current = head; // Pointer to traverse the linked list
Node* reversedPart = NULL; // Pointer to store the reversed portion of the list
int remainingRotations = k; // Counter for the number of rotations
Node* lastNode = head;
// Traverse to the end of the list to find the last node
while (lastNode->next != NULL) {
lastNode = lastNode->next;
}
// Perform the rotation for the specified number of times
while (remainingRotations != 0 && current != NULL) {
Node* nextNode = current->next; // Store the next node
head = nextNode; // Move the head to the next node
current->next = reversedPart; // Reverse the current node's next pointer
lastNode->next = current; // Attach the reversed node at the end of the list
lastNode = lastNode->next; // Move to the new last node
current = nextNode; // Move to the next node
remainingRotations--; // Decrease the number of rotations left
}
return head; // Return the new head of the rotated list
}
};
class Solution:
def rotate(self, head, k):
current = head # Pointer to traverse the linked list
reversedPart = None # Pointer to store the reversed portion of the list
remainingRotations = k # Counter for the number of rotations
# Find the last node of the list
lastNode = head
while lastNode.next is not None:
lastNode = lastNode.next
# Perform the rotation for the specified number of times
while remainingRotations != 0 and current is not None:
nextNode = current.next # Store the next node
head = nextNode # Move the head to the next node
current.next = reversedPart # Reverse the current node's next pointer
lastNode.next = current # Attach the reversed node at the end of the list
lastNode = lastNode.next # Move to the new last node
current = nextNode # Move to the next node
remainingRotations -= 1 # Decrease the number of rotations left
return head # Return the new head of the rotated list
Time Complexity
- Traversing to the End:
The algorithm first traverses to the end of the linked list to find the last node. This operation takes \( O(n) \) time, where \( n \) is the number of nodes in the linked list.
- Performing Rotations:
The algorithm then performs rotations by moving nodes and updating pointers. Each rotation involves constant time operations, and the number of rotations is limited by \( k \). Therefore, in the worst case where \( k \) is equal to the number of nodes \( n \), this part also takes \( O(n) \) time.
- Overall Time Complexity:
The overall time complexity of the algorithm is \( O(n) \), considering both traversing to the end of the list and performing rotations.
Space Complexity
- Additional Space:
The algorithm uses a few extra pointers (`current`, `reversedPart`, `lastNode`, and `nextNode`). These pointers require constant space \( O(1) \), regardless of the number of nodes in the list.
- Overall Space Complexity:
The overall space complexity of the algorithm is \( O(1) \), as it uses a constant amount of extra space.