You are given an Undirected Graph having unit weight of the edges, find the shortest pathfrom src to all the vertex and if it is unreachable to reach any vertex, then return -1 for that vertex.
Examples :
Input: n = 9, m = 10 edges=[[0,1],[0,3],[3,4],[4,5],[5,6],[1,2],[2,6],[6,7],[7,8],[6,8]] src=0 Output: 0 1 2 1 2 3 3 4 4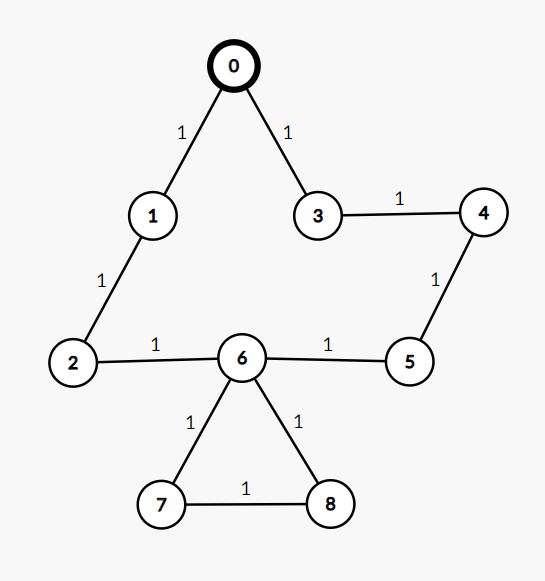
Input: n = 4, m = 2 edges=[[1,3],[3,0]] src=3 Output: 1 1 -1 0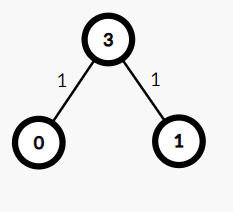
Constraint:
1<=n,m<=104
0<=edges[i][j]<=n-1
Expected Time Complexity: O(N + E), where N is the number of nodes and E is the edges
Expected Space Complexity: O(N)
Approach 01:
-
C++
-
Python
#include <vector>
#include <queue>
#include <limits>
class Solution {
public:
std::vector<int> shortestPath(std::vector<std::vector<int>>& edges, int numNodes, int numEdges, int source) {
// Create an adjacency list for the graph
std::vector<std::vector<int>> adjacencyList(numNodes);
for (const auto& edge : edges) {
int u = edge[0];
int v = edge[1];
adjacencyList[u].push_back(v);
adjacencyList[v].push_back(u);
}
// Initialize distance array with infinity, except for the source node
std::vector<int> distances(numNodes, std::numeric_limits<int>::max());
distances[source] = 0;
// Perform BFS starting from the source node
std::queue<int> queue;
queue.push(source);
while (!queue.empty()) {
int currentNode = queue.front();
queue.pop();
for (int neighbor : adjacencyList[currentNode]) {
if (distances[neighbor] == std::numeric_limits<int>::max()) { // Not visited
distances[neighbor] = distances[currentNode] + 1;
queue.push(neighbor);
}
}
}
// Replace 'infinity' with -1 for nodes that are unreachable from the source
for (int& distance : distances) {
if (distance == std::numeric_limits<int>::max()) {
distance = -1;
}
}
return distances;
}
};
from collections import deque
class Solution:
def shortestPath(self, edges, numNodes, numEdges, source):
# Create an adjacency list for the graph
adjacencyList = [[] for _ in range(numNodes)]
for u, v in edges:
adjacencyList[u].append(v)
adjacencyList[v].append(u)
# Initialize distance array with infinity, except for the source node
distances = [float('inf')] * numNodes
distances[source] = 0
# Perform BFS starting from the source node
queue = deque([source])
while queue:
currentNode = queue.popleft()
for neighbor in adjacencyList[currentNode]:
if distances[neighbor] == float('inf'): # Not visited
distances[neighbor] = distances[currentNode] + 1
queue.append(neighbor)
# Replace 'inf' with -1 for nodes that are unreachable from the source
distances = [-1 if distance == float('inf') else distance for distance in distances]
return distances
Time Complexity
- Building the Adjacency List:
Constructing the adjacency list involves iterating through all edges, which takes \( O(\text{numEdges}) \) time.
- Breadth-First Search (BFS):
The BFS traverses each node and edge once. The time complexity of BFS is \( O(\text{numNodes} + \text{numEdges}) \), where \(\text{numNodes}\) is the number of nodes and \(\text{numEdges}\) is the number of edges.
- Overall Time Complexity:
The overall time complexity is \( O(\text{numNodes} + \text{numEdges}) \), accounting for both the adjacency list construction and the BFS traversal.
Space Complexity
- Adjacency List:
The adjacency list requires \( O(\text{numNodes} + \text{numEdges}) \) space. Each node’s adjacency list stores all its edges, summing up to the total number of edges.
- Distance Array:
The distance array requires \( O(\text{numNodes}) \) space to store the shortest path distances for each node.
- Queue:
The queue used in BFS can hold up to \( O(\text{numNodes}) \) nodes at a time in the worst case.
- Overall Space Complexity:
The overall space complexity is \( O(\text{numNodes} + \text{numEdges}) \), dominated by the adjacency list and the BFS queue.