590. N-ary Tree Postorder Traversal

Given the root of an n-ary tree, return the postorder traversal of its nodes’ values.

Nary-Tree input serialization is represented in their level order traversal. Each group of children is separated by the null value (See examples)

Example 1:

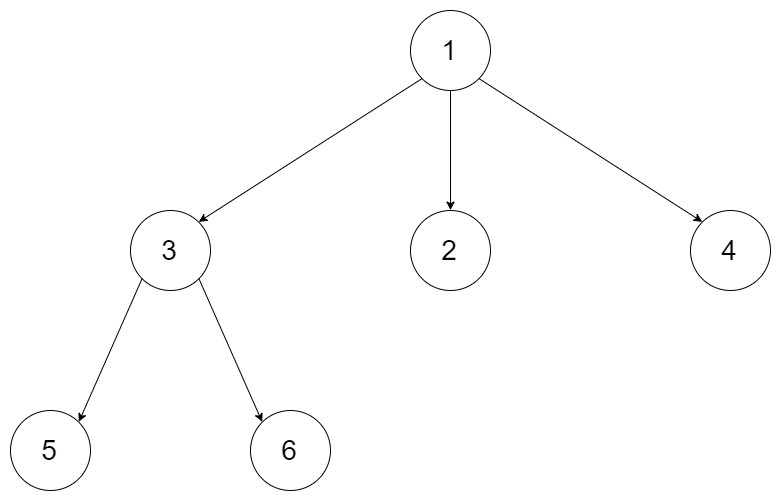
Input: root = [1,null,3,2,4,null,5,6]
Output: [5,6,3,2,4,1]

Example 2:

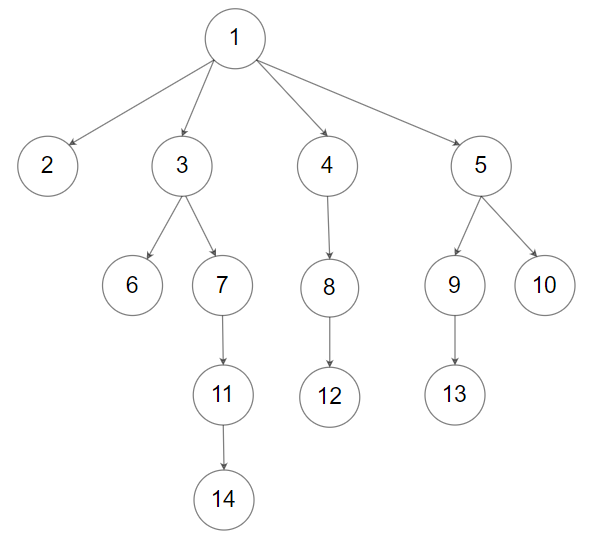
Input: root = [1,null,2,3,4,5,null,null,6,7,null,8,null,9,10,null,null,11,null,12,null,13,null,null,14]
Output: [2,6,14,11,7,3,12,8,4,13,9,10,5,1]

Constraints:

• The number of nodes in the tree is in the range [0, 104].
• 0 <= Node.val <= 104
• The height of the n-ary tree is less than or equal to 1000.

Approach 01:

class Solution {
    public:
    vector<int> postorder(Node* root) {
        if (root == nullptr){
            return {};
        }

        vector<int> result;
        stack<Node*> stack{{root}};

        while (!stack.empty()) {
            root = stack.top(), stack.pop();
            result.push_back(root->val);
            for (Node* child : root->children){
                stack.push(child);
            }
        }

        ranges::reverse(result);
        return result;
    }
};

class Solution:
    def postorder(self, root: 'Node') -> list[int]:
        if not root:
            return []

        result = []
        stack = [root]

        while stack:
            node = stack.pop()
            result.append(node.val)
            for child in node.children:
                stack.append(child)

        result.reverse()
        return result

Time Complexity

• Traversal:

  The function processes each node of the n-ary tree exactly once. Since there are \( n \) nodes in the tree, the time complexity is \( O(n) \).

• Reversing the Result:

  After traversing the tree, the function reverses the result vector, which also takes \( O(n) \) time.

• Overall Time Complexity:

  The overall time complexity is \( O(n) \), combining the time to traverse the tree and reverse the result vector.

Space Complexity

• Stack:

  The stack can hold up to \( O(n) \) nodes in the worst case (e.g., if the tree is highly unbalanced). Thus, the space complexity due to the stack is \( O(n) \).

• Result Vector:

  The result vector stores the values of all nodes, requiring \( O(n) \) space.

• Overall Space Complexity:

  The overall space complexity is \( O(n) \), considering both the stack and the result vector.