Given a Binary Tree (BT), convert it to a Doubly Linked List (DLL) in place. The left and right pointers in nodes will be used as previous and next pointers respectively in converted DLL. The order of nodes in DLL must be the same as the order of the given Binary Tree. The first node of Inorder traversal (leftmost node in BT) must be the head node of the DLL.
Note: h is the tree’s height, and this space is used implicitly for the recursion stack.
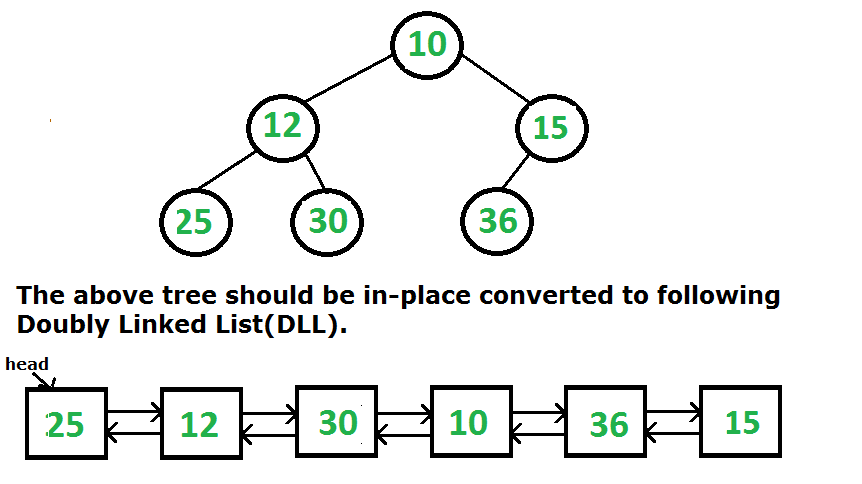
Examples:
Input: 1 / \ 3 2 Output:
3 1 2 2 1 3Explanation: DLL would be 3<=>1<=>2
Input:
10
/ \
20 30
/ \
40 60
Output:
40 20 60 10 30
30 10 60 20 40

Explanation: DLL would be 40<=>20<=>60<=>10<=>30.
Expected Time Complexity: O(no. of nodes)
Expected Space Complexity: O(height of the tree)
Constraints:
1 ≤ Number of nodes ≤ 105
0 ≤ Data of a node ≤ 105
Approach 01:
-
C++
-
Python
class Solution {
public:
Node* head=NULL;
Node* tail=NULL;
void solve(Node* root){
if(root==NULL){
return;
}
solve(root->left);
if(head==NULL){
head=tail=root;
}
else{
tail->right=root;
root->left=tail;
}
tail=root;
solve(root->right);
}
Node* bToDLL(Node* root) {
solve(root);
return head;
}
};
class Solution:
def __init__(self):
self.head = None
self.tail = None
def solve(self, root):
if root is None:
return
# Recursively convert the left subtree
self.solve(root.left)
# If this is the first node (leftmost), it becomes the head
if self.head is None:
self.head = self.tail = root
else:
# Attach the current root to the DLL
self.tail.right = root
root.left = self.tail
# Move the tail pointer to the current node
self.tail = root
# Recursively convert the right subtree
self.solve(root.right)
def bToDLL(self, root):
self.solve(root)
return self.head
Time Complexity
- In-Order Traversal:
The algorithm performs an in-order traversal of the binary tree, visiting each node exactly once. Since there are
nnodes in the tree, the traversal takes \(O(n)\). - Updating Pointers:
For each node, the algorithm updates its left and right pointers, which is an \(O(1)\) operation. As this is done for each of the
nnodes, it also contributes \(O(n)\) to the total time complexity. - Overall Time Complexity:
The overall time complexity is \(O(n)\), where
nis the number of nodes in the binary tree.
Space Complexity
- Space for Recursion Stack:
The algorithm uses recursion to traverse the tree. In the worst case, the recursion stack depth can be equal to the height of the tree. For a balanced binary tree, this height is \(O(\log n)\), and for a skewed binary tree, the height is \(O(n)\).
- Space for Variables:
A few pointers (`head`, `tail`, `root`) are used to keep track of nodes during the conversion. These take \(O(1)\) extra space.
- Overall Space Complexity:
The overall space complexity is \(O(h)\), where
his the height of the tree. In the worst case (skewed tree), this could be \(O(n)\), and in the best case (balanced tree), it could be \(O(\log n)\).