Clone A Linked List With Next And Random Pointer

You are given a special linked list where each node has a next pointer pointing to its next node. You are also given some random pointers, where you will be givensome pairs denoting two nodes a and b i.e. a->random = b(randomis a pointer to a random node).

Construct a copy of the given list. The copy should consist of the same number of new nodes, where each new node has its value set to the value of its corresponding original node. Both the next and random pointer of the new nodes should point to new nodes in the copied list such that the original and copied list pointers represent the same list state. None of the pointers in the new list should point to nodes in the original list.

For example, if there are two nodes x and y in the original list, where x->random = y, then for the corresponding two nodes x_new and y_new in the copied list, x_new->random = y_new.

Return the head of the copied linked list.

NOTE : 
1. If there is any node whose arbitrary pointer is not given then it’s by default NULL. 
2. Don’t make any changes to the original linked list.

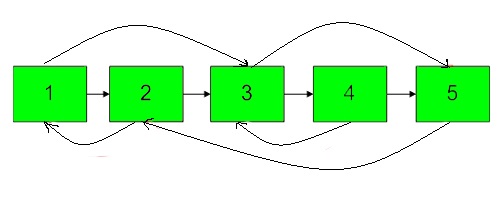
Note: The diagram isn’t part of any example, it just depicts an example of how the linked list may look.

Examples:

Input: LinkedList: 1->2->3->4 , pairs = [{1,2},{2,4}]
Output: true
Explanation: In this test case, there are 4 nodes in linked list. Among these 4 nodes, 2 nodes have arbitrary pointer set, rest two nodes have arbitrary pointer as NULL. Second line tells us the value of four nodes. The third line gives the information about arbitrary pointers. The first node arbitrary pointer is set to node 2. The second node arbitrary pointer is set to node 4.

Input: LinkedList: 1->3->5->9 , pairs[] = [{1,1},{3,4}]
Output: true
Explanation: In the given testcase, applying the method as stated in the above example, the output will be 1.

Expected Time Complexity: O(n)
Expected Auxilliary Space: O(1)

Constraints:
1 <= numbers of random pointer <= number of nodes <= 100
0 <= node->data <= 1000
1 <= a, b <= 100

Approach 01:

class Solution {
public:
    Node* copyList(Node* head) {
        // Map to store the original node to its copy
        unordered_map<Node*, Node*> nodeMap;
        Node* currentNode = head;
        
        // First pass: Create new nodes and store them in the map
        while (currentNode) {
            nodeMap[currentNode] = new Node(currentNode->data);
            currentNode = currentNode->next;
        }
        
        currentNode = head;
        
        // Second pass: Assign next and random pointers for the copied nodes
        while (currentNode) {
            nodeMap[currentNode]->next = currentNode->next ? nodeMap[currentNode->next] : nullptr;
            nodeMap[currentNode]->random = currentNode->random ? nodeMap[currentNode->random] : nullptr;
            currentNode = currentNode->next;
        }
        
        // Return the head of the copied list
        return nodeMap[head];
    }
};

class Solution:
    def copyList(self, head: 'Node') -> 'Node':
        # Dictionary to map original nodes to their copies
        nodeMap = {}
        currentNode = head

        # First pass: Create new nodes and store them in the map
        while currentNode:
            nodeMap[currentNode] = Node(currentNode.data)
            currentNode = currentNode.next

        currentNode = head

        # Second pass: Assign next and random pointers for the copied nodes
        while currentNode:
            nodeMap[currentNode].next = nodeMap[currentNode.next] if currentNode.next else None
            nodeMap[currentNode].random = nodeMap[currentNode.random] if currentNode.random else None
            currentNode = currentNode.next

        # Return the head of the copied list
        return nodeMap[head] if head else None

Time Complexity

• First Pass (Creating Copies):

  In the first pass, we iterate through the entire linked list once to create new nodes and store them in the hash map. This takes \(O(n)\), where \(n\) is the number of nodes in the original list.

• Second Pass (Assigning Next and Random Pointers):

  In the second pass, we again iterate through the linked list to assign the `next` and `random` pointers for each copied node. This also takes \(O(n)\).

• Overall Time Complexity:

  Since both passes take \(O(n)\), the overall time complexity is \(O(n)\), where \(n\) is the number of nodes in the linked list.

Space Complexity

• Hash Map:

  The hash map stores a mapping from each original node to its copy, which requires \(O(n)\) space, where \(n\) is the number of nodes in the linked list.

• New Nodes:

  In addition to the hash map, we also create a new copy of the linked list, which takes up \(O(n)\) space.

• Overall Space Complexity:

  The overall space complexity is \(O(n)\), due to the hash map and the new linked list.