Given a connected undirected graph represented by a 2-d adjacency list adj[][], where each adj[i] represents the list of vertices connected to vertex i. Perform a Depth First Search (DFS) traversal starting from vertex 0, visiting vertices from left to right as per the given adjacency list, and return a list containing the DFS traversal of the graph.
Note: Do traverse in the same order as they are in the given adjacency list.
Examples:
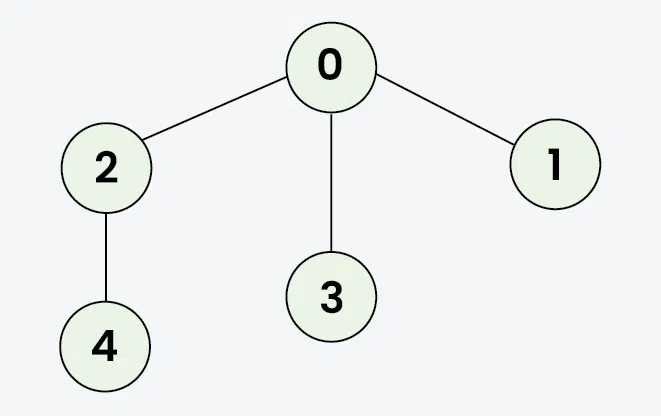
Input: adj[][] = [[2, 3, 1], [0], [0, 4], [0], [2]]
Output: [0, 2, 4, 3, 1]
Explanation: Starting from 0, the DFS traversal proceeds as follows:
Visit 0 → Output: 0
Visit 2 (the first neighbor of 0) → Output: 0, 2
Visit 4 (the first neighbor of 2) → Output: 0, 2, 4
Backtrack to 2, then backtrack to 0, and visit 3 → Output: 0, 2, 4, 3
Finally, backtrack to 0 and visit 1 → Final Output: 0, 2, 4, 3, 1
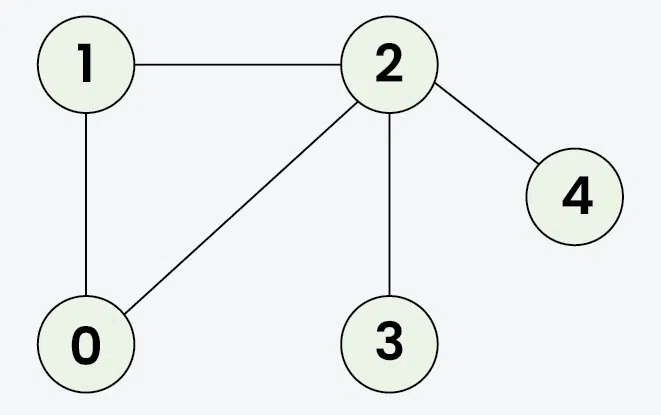
Input: adj[][] = [[1, 2], [0, 2], [0, 1, 3, 4], [2], [2]]
Output: [0, 1, 2, 3, 4] Explanation: Starting from 0, the DFS traversal proceeds as follows:
Visit 0 → Output: 0
Visit 1 (the first neighbor of 0) → Output: 0, 1
Visit 2 (the first neighbor of 1) → Output: 0, 1, 2
Visit 3 (the first neighbor of 2) → Output: 0, 1, 2, 3
Backtrack to 2 and visit 4 → Final Output: 0, 1, 2, 3, 4
Constraints:
1 ≤ adj.size() ≤ 104
1 ≤ adj[i][j] ≤ 104
Approach 01:
-
C++
-
Python
#include <vector>
using namespace std;
class Solution {
public:
void dfsHelper(int node, vector<vector<int>>& adjacencyList, vector<int>& visited, vector<int>& traversalResult) {
visited[node] = 1;
traversalResult.push_back(node);
for (auto& neighbor : adjacencyList[node]) {
if (!visited[neighbor]) {
dfsHelper(neighbor, adjacencyList, visited, traversalResult);
}
}
}
vector<int> dfs(vector<vector<int>>& adjacencyList) {
int numVertices = adjacencyList.size();
vector<int> visited(numVertices, 0);
vector<int> traversalResult;
int startNode = 0;
dfsHelper(startNode, adjacencyList, visited, traversalResult);
return traversalResult;
}
};
from typing import List
class Solution:
def dfsHelper(self, node: int, adjacencyList: List[List[int]], visited: List[bool], traversalResult: List[int]) -> None:
visited[node] = True
traversalResult.append(node)
for neighbor in adjacencyList[node]:
if not visited[neighbor]:
self.dfsHelper(neighbor, adjacencyList, visited, traversalResult)
def dfs(self, adjacencyList: List[List[int]]) -> List[int]:
numVertices = len(adjacencyList)
visited = [False] * numVertices
traversalResult = []
startNode = 0
self.dfsHelper(startNode, adjacencyList, visited, traversalResult)
return traversalResult
Time Complexity:
- Depth-First Search Traversal:
Each vertex is visited once, and each edge is explored once, leading to a total complexity of \( O(V + E) \), where \( V \) is the number of vertices and \( E \) is the number of edges.
- Recursive Calls:
Each recursive call processes one vertex and explores its neighbors, but since each edge is traversed once, the recursion itself remains within \( O(V + E) \).
- Total Time Complexity:
The overall time complexity is \( O(V + E) \).
Space Complexity:
- Visited Array:
The
visitedarray stores information for each vertex, consuming \( O(V) \) space. - Traversal Result:
The
traversalResultstores all visited nodes, requiring \( O(V) \) space. - Recursive Stack:
In the worst case (a linear graph), the recursive stack depth reaches \( O(V) \).
- Total Space Complexity:
Since all dominant terms are \( O(V) \), the overall space complexity is \( O(V) \).