Diameter of a Binary Tree

Given a binary tree, the diameter (also known as the width) is defined as the number of edges on the longest path between two leaf nodes in the tree. This path may or may not pass through the root. Your task is to find the diameter of the tree.

Examples:

Input:

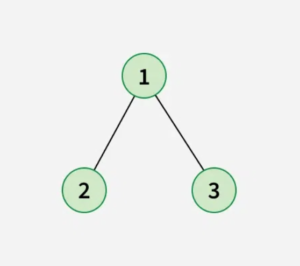
root[] = [1, 2, 3]

Output:

2

Explanation:

The longest path has 2 edges (node 2 -> node 1 -> node 3).

Input:

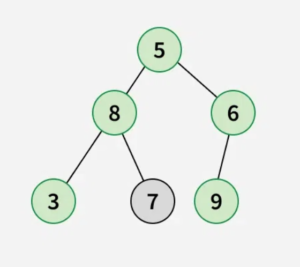
root[] = [5, 8, 6, 3, 7, 9]

Output:

4

Explanation:

The longest path has 4 edges (node 3 -> node 8 -> node 5 -> node 6 -> node 9).

Constraints:
1 ≤ number of nodes ≤ 10⁵
0 ≤ node->data ≤ 10⁵

Approach 01:

class Solution {
  public:
    int height(Node * root, int& maxDiameter) {
        if (root == NULL) {
            return 0;
        }
        
        int leftHeight = height(root->left, maxDiameter);
        int rightHeight = height(root->right, maxDiameter);
        maxDiameter = max(maxDiameter, leftHeight + rightHeight);
        return max(leftHeight, rightHeight) + 1;
    }

    int diameter(Node* root) {
        int maxDiameter = INT_MIN;
        height(root, maxDiameter);
        return maxDiameter;
    }
};

class Solution:
    def height(self, root, maxDiameter):
        if root is None:
            return 0
        
        leftHeight = self.height(root.left, maxDiameter)
        rightHeight = self.height(root.right, maxDiameter)
        maxDiameter[0] = max(maxDiameter[0], leftHeight + rightHeight)
        return max(leftHeight, rightHeight) + 1

    def diameter(self, root):
        maxDiameter = [-float('inf')]  # Use list to modify inside recursion
        self.height(root, maxDiameter)
        return maxDiameter[0]

Time Complexity:

• Recursive Traversal:Each node is visited once to compute its height, leading to a recurrence relation similar to \( T(N) = 2T(N/2) + O(1) \).
• Overall Time Complexity:\( O(N) \), where \( N \) is the number of nodes in the tree.

Space Complexity:

• Recursive Stack:In the worst case (a skewed tree), the recursion depth reaches \( O(N) \). In a balanced tree, it is \( O(\log N) \).
• Auxiliary Space:Only a few integer variables (maxDiameter, leftHeight, rightHeight) are used, contributing to \( O(1) \) space.
• Overall Space Complexity:Worst case: \( O(N) \), Best case: \( O(\log N) \).