Given the head of a linked list, determine whether the list contains a loop. If a loop is present, return the number of nodes in the loop, otherwise return 0.

Note: ‘c‘ is the position of the node which is the next pointer of the last node of the linkedlist. If c is 0, then there is no loop.
Examples:
Input: LinkedList: 25->14->19->33->10->21->39->90->58->45, c = 4 Output: 7 Explanation: The loop is from 33 to 45. So length of loop is 33->10->21->39-> 90->58->45 = 7.
The number 33 is connected to the last node of the linkedlist to form the loop because according to the input the 4th node from the beginning(1 based indexing)
will be connected to the last node for the loop.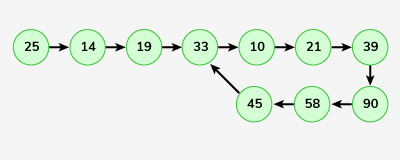
Input: LinkedList: 5->4, c = 0 Output: 0 Explanation: There is no loop.
Expected Time Complexity: O(n)
Expected Auxiliary Space: O(1)
Constraints:
1 <= no. of nodes <= 106
0 <= node.data <=106
0 <= c<= n-1
Approach 01:
-
C++
-
Python
#include <iostream>
#include <unordered_map>
using namespace std;
class Solution {
public:
// Function to find the length of a loop in the linked list.
int countNodesinLoop(Node *head) {
int position = 0;
unordered_map<Node*, int> nodePositionMap;
while (head != nullptr) {
// Check if the node has been visited before, indicating a loop
if (nodePositionMap.find(head) != nodePositionMap.end()) {
// Calculate the loop length by subtracting the stored position
return position - nodePositionMap[head];
} else {
// Store the current node with its position
nodePositionMap[head] = position++;
head = head->next;
}
}
// Return 0 if no loop is detected
return 0;
}
};
class Solution:
# Function to find the length of a loop in the linked list.
def countNodesInLoop(self, head):
position = 0
nodePositionMap = {}
while head:
if head in nodePositionMap:
# Calculate the loop length by subtracting the stored position.
return position - nodePositionMap[head]
else:
# Store the current node with its position.
nodePositionMap[head] = position
position += 1
head = head.next
# Return 0 if no loop is detected.
return 0
Time Complexity
- Traversal of Nodes:
Each node in the linked list is visited once until a loop is detected or the end of the list is reached. Therefore, the traversal takes \( O(\text{numNodes}) \) time, where
numNodesis the total number of nodes in the linked list. - Overall Time Complexity:
The overall time complexity is \( O(\text{numNodes}) \), as the algorithm only involves traversing the list and storing nodes in a map.
Space Complexity
- Node Position Map:
The unordered map
nodePositionMapstores each node and its position until a loop is detected. In the worst case, if there is no loop, the map stores all nodes, leading to a space complexity of \( O(\text{numNodes}) \). - Overall Space Complexity:
The overall space complexity is \( O(\text{numNodes}) \), primarily due to the unordered map used to store nodes and their positions.
