Find the number of islands

Given a grid of size n*m (n is the number of rows and m is the number of columns in the grid) consisting of ‘W’s (Water) and ‘L’s (Land). Find the number of islands.

Note: An island is either surrounded by water or the boundary of a grid and is formed by connecting adjacent lands horizontally or vertically or diagonally i.e., in all 8 directions.

Examples:

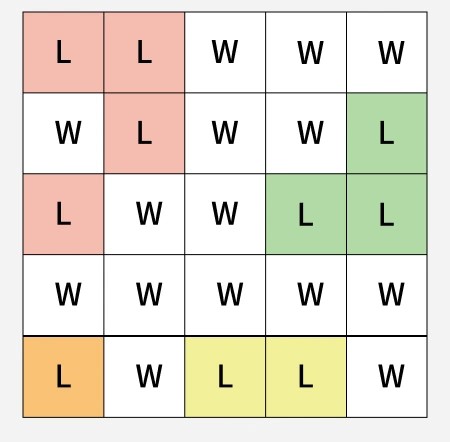
Input: grid[][] = [['L', 'L', 'W', 'W', 'W'], ['W', 'L', 'W', 'W', 'L'], ['L', 'W', 'W', 'L', 'L'], ['W', 'W', 'W', 'W', 'W'], ['L', 'W', 'L', 'L', 'W']]
Output: 4
Explanation:
The image below shows all the 4 islands in the grid.

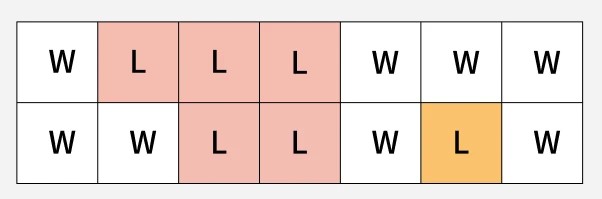
Input: grid[][] = [['W', 'L', 'L', 'L', 'W', 'W', 'W'], ['W', 'W', 'L', 'L', 'W', 'L', 'W']]
Output: 2
Expanation:
The image below shows 2 islands in the grid.

Constraints:
1 ≤ n, m ≤ 500
grid[i][j] = {‘L’, ‘W’}

Approach 01:

#include <vector>
#include <queue>

using namespace std;

class Solution {
public:
    int countIslands(vector<vector<char>>& grid) {
        int deltaX[8] = {0, 0, 1, -1, 1, 1, -1, -1};
        int deltaY[8] = {1, -1, 0, 0, -1, 1, -1, 1};
        int rows = grid.size();
        int cols = grid[0].size();
        int islandCount = 0;

        for (int row = 0; row < rows; row++) {
            for (int col = 0; col < cols; col++) {
                if (grid[row][col] == 'L') {
                    queue<pair<int, int>> bfsQueue;
                    bfsQueue.push({row, col});
                    grid[row][col] = 'W';
                    islandCount++;

                    while (!bfsQueue.empty()) {
                        auto currentCell = bfsQueue.front();
                        bfsQueue.pop();

                        for (int dir = 0; dir < 8; dir++) {
                            int newRow = currentCell.first + deltaX[dir];
                            int newCol = currentCell.second + deltaY[dir];

                            if (newRow >= 0 && newRow < rows &&
                                newCol >= 0 && newCol < cols &&
                                grid[newRow][newCol] == 'L') {
                                bfsQueue.push({newRow, newCol});
                                grid[newRow][newCol] = 'W';
                            }
                        }
                    }
                }
            }
        }

        return islandCount;
    }
};

from collections import deque
from typing import List

class Solution:
    def numIslands(self, grid: List[List[str]]) -> int:
        deltaX = [0, 0, 1, -1, 1, 1, -1, -1]
        deltaY = [1, -1, 0, 0, -1, 1, -1, 1]
        rows = len(grid)
        cols = len(grid[0])
        islandCount = 0

        for row in range(rows):
            for col in range(cols):
                if grid[row][col] == 'L':
                    bfsQueue = deque()
                    bfsQueue.append((row, col))
                    grid[row][col] = 'W'
                    islandCount += 1

                    while bfsQueue:
                        currentRow, currentCol = bfsQueue.popleft()

                        for direction in range(8):
                            newRow = currentRow + deltaX[direction]
                            newCol = currentCol + deltaY[direction]

                            if 0 <= newRow < rows and 0 <= newCol < cols and grid[newRow][newCol] == 'L':
                                bfsQueue.append((newRow, newCol))
                                grid[newRow][newCol] = 'W'

        return islandCount

Time Complexity:

• Outer Grid Traversal:

  Each cell in the grid is visited once, giving a base complexity of \( O(M \times N) \), where \( M \) is the number of rows and \( N \) is the number of columns.

• BFS Traversal:

  Each land cell is visited once during BFS and marked as water to avoid revisiting, so total BFS work across all islands is still \( O(M \times N) \).

• Total Time Complexity:

  The overall time complexity is \( O(M \times N) \).

Space Complexity:

• BFS Queue:

  In the worst case, the queue can hold all land cells, contributing up to \( O(M \times N) \) space.

• In-Place Grid Modification:

  No extra visited array is used; the input grid is modified in-place.

• Total Space Complexity:

  The space complexity is \( O(M \times N) \) due to the queue.