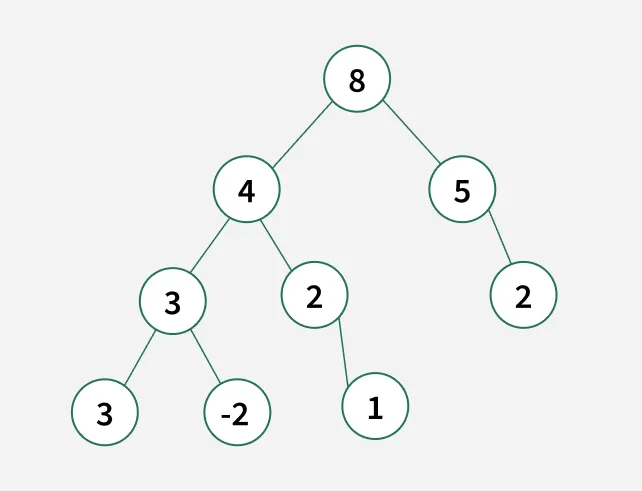
Given a binary tree and an integer k, determine the number of downward-only paths where the sum of the node values in the path equals k. A path can start and end at any node within the tree but must always move downward (from parent to child).
Examples:
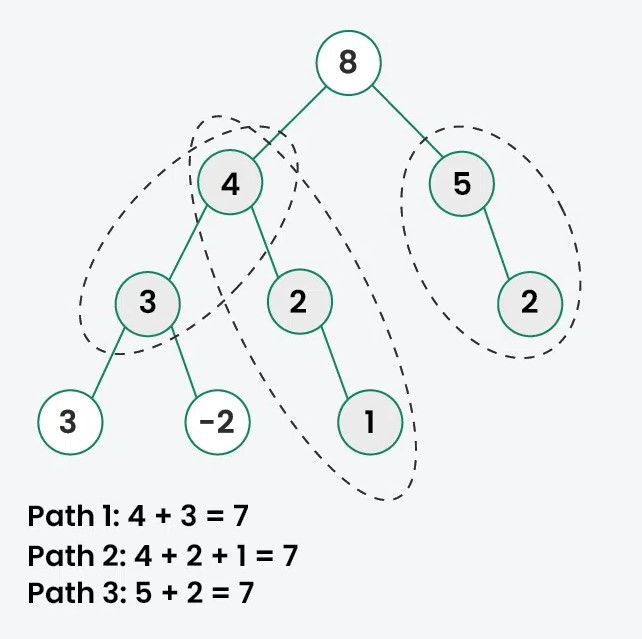
Input: k = 7
Output: 3 Explanation: The following paths sum to k
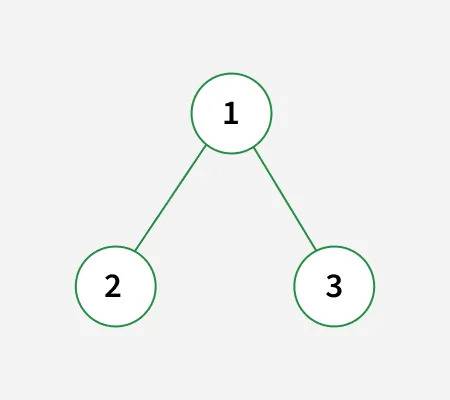
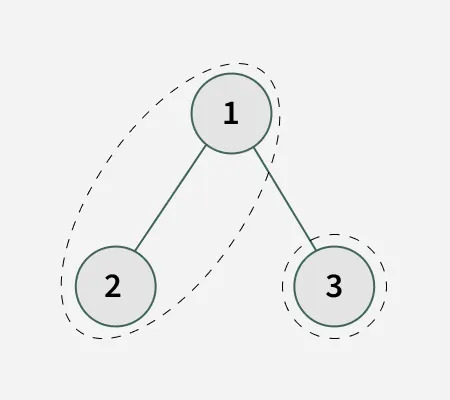
Input: k = 3
Output: 2 Explanation: Path 1 : 1 -> 2 (Sum = 3) Path 2 : 3 (Sum = 3)
Constraints:
- 1 ≤ number of nodes ≤ 104
- -100 ≤ node value ≤ 100
- -109 ≤ k ≤ 109
Approach 01:
-
C++
-
Python
#include <unordered_map>
using namespace std;
class Solution {
public:
void solve(Node* node, int currentSum, int targetSum, unordered_map<int, int> &prefixSumMap, int &pathCount) {
if (!node)
return;
currentSum += node->data;
if (currentSum == targetSum)
pathCount++;
pathCount += prefixSumMap[currentSum - targetSum];
prefixSumMap[currentSum]++;
solve(node->left, currentSum, targetSum, prefixSumMap, pathCount);
solve(node->right, currentSum, targetSum, prefixSumMap, pathCount);
prefixSumMap[currentSum]--; // Backtrack
}
int sumK(Node* root, int targetSum) {
int pathCount = 0;
unordered_map<int, int> prefixSumMap;
solve(root, 0, targetSum, prefixSumMap, pathCount);
return pathCount;
}
};
from collections import defaultdict
class Solution:
def solve(self, node, currentSum, targetSum, prefixSumMap, pathCount):
if not node:
return
currentSum += node.data
if currentSum == targetSum:
pathCount[0] += 1
pathCount[0] += prefixSumMap[currentSum - targetSum]
prefixSumMap[currentSum] += 1
self.solve(node.left, currentSum, targetSum, prefixSumMap, pathCount)
self.solve(node.right, currentSum, targetSum, prefixSumMap, pathCount)
prefixSumMap[currentSum] -= 1
def sumK(self, root, targetSum):
pathCount = [0]
prefixSumMap = defaultdict(int)
self.solve(root, 0, targetSum, prefixSumMap, pathCount)
return pathCount[0]
Time Complexity:
- Tree Traversal:
Each node is visited once, leading to a complexity of \( O(N) \), where \( N \) is the number of nodes in the tree.
- Prefix Sum Operations:
Each node performs constant-time operations (\( O(1) \)) involving the prefix sum map.
- Overall Time Complexity:
\( O(N) \), since each node is processed in constant time.
Space Complexity:
- Recursive Stack:
In the worst case (skewed tree), the recursion depth is \( O(N) \), while in a balanced tree, it is \( O(\log N) \).
- Prefix Sum Map:
In the worst case, the map stores a sum for each node, taking \( O(N) \) space.
- Overall Space Complexity:
Worst case: \( O(N) \), Best case (balanced tree): \( O(\log N) \).