Linked List Matrix

Given a Matrix mat of n*n size. Your task is constructing a 2D linked list representation of the given matrix.

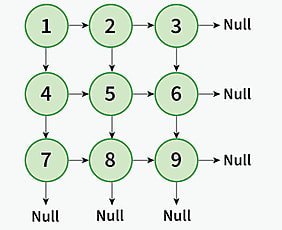
Input: mat = [[1, 2, 3], [4, 5, 6], [7, 8, 9]]
Output: 

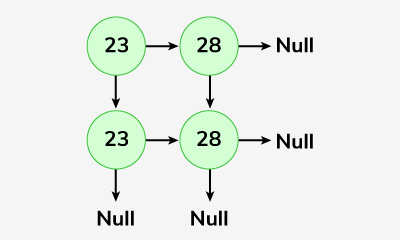
Input: mat = [[23, 28], [23, 28]]
Output:

Expected Time Complexity: O(n²)
Expected Space Complexity: O(n²)

Constraints:
1 <= mat.size() <=15
1 <= mat[i][j] <=10⁴

Approach 01:

class Solution {
public:
    Node* constructLinkedMatrix(vector<vector<int>>& mat) {
        int rows = mat.size();
        int cols = mat[0].size();

        Node* head = new Node(mat[0][0]);
        Node* currentRowNode = head;

        for (int i = 0; i < rows; ++i) {
            Node* currentColumnNode = currentRowNode;

            for (int j = 0; j < cols; ++j) {
                // Create and link the right node
                if (j + 1 < cols) {
                    currentColumnNode->right = new Node(mat[i][j + 1]);
                }

                // Create and link the down node
                if (i + 1 < rows) {
                    currentColumnNode->down = new Node(mat[i + 1][j]);
                }

                currentColumnNode = currentColumnNode->right;
            }

            // Move to the next row
            currentRowNode = currentRowNode->down;
        }

        return head;
    }
};

class Solution:
    def constructLinkedMatrix(self, mat):
        rows = len(mat)
        cols = len(mat[0])

        head = Node(mat[0][0])
        currentRowNode = head

        for i in range(rows):
            currentColumnNode = currentRowNode

            for j in range(cols):
                # Create and link the right node
                if j + 1 < cols:
                    currentColumnNode.right = Node(mat[i][j + 1])

                # Create and link the down node
                if i + 1 < rows:
                    currentColumnNode.down = Node(mat[i + 1][j])

                currentColumnNode = currentColumnNode.right

            # Move to the next row
            currentRowNode = currentRowNode.down

        return head

Time Complexity

• Node creation and linking:

  The function iterates through each element in the 2D matrix once. For each element, it creates a new node and links it either to the right or down, which takes constant time for each element. Since there are \(m \times n\) elements in the matrix, where \(m\) is the number of rows and \(n\) is the number of columns, the time complexity is \(O(m \times n)\).

• Overall Time Complexity:

  The overall time complexity is \(O(m \times n)\), where \(m\) is the number of rows and \(n\) is the number of columns in the matrix.

Space Complexity

• Auxiliary Space:

  The function creates one new node for each element in the matrix. Thus, the space complexity for storing the nodes is \(O(m \times n)\), where \(m\) is the number of rows and \(n\) is the number of columns.

• Overall Space Complexity:

  The overall space complexity is \(O(m \times n)\), due to the memory required to store all the nodes in the linked matrix.