Mirror Tree

Given a Binary Tree, convert it into its mirror.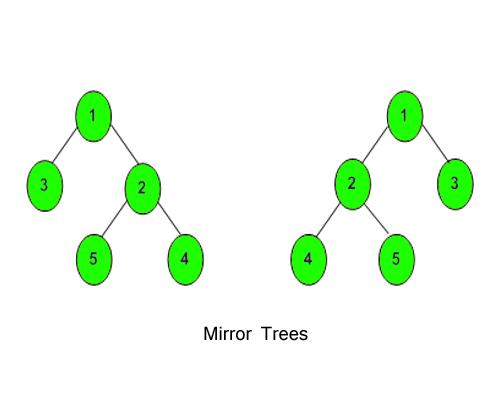
            

Examples:

Input:
      1
    /  \
   2    3
Output: 3 1 2
Explanation: The tree is
   1    (mirror)  1
 /  \    =>      /  \
2    3          3    2
The inorder of mirror is 3 1 2

Input:
      10
     /  \
    20   30
   /  \
  40  60
Output: 30 10 60 20 40
Explanation: The tree is
      10               10
    /    \  (mirror) /    \
   20    30    =>   30    20
  /  \                   /   \
 40  60                 60   40
The inroder traversal of mirror is
30 10 60 20 40.

Expected Time Complexity: O(N).
Expected Auxiliary Space: O(Height of the Tree).

Constraints:
1 ≤ Number of nodes ≤ 10⁵
1 ≤ Data of a node ≤ 10⁵

Approach 01

class Solution {
  public:
    // Function to convert a binary tree into its mirror tree.
    void mirror(Node* node) {
        // code here
        if(!node){
            return;
        }
        
        Node* temp = node->left;
        node->left = node->right;
        node->right = temp;
        
        mirror(node->left);
        mirror(node->right);
    }
};

class Solution:
    # Function to convert a binary tree into its mirror tree.
    def mirror(self, node):
        # Base case: if the node is None, return
        if not node:
            return
        
        # Swap the left and right children
        temp = node.left
        node.left = node.right
        node.right = temp
        
        # Recursively mirror the left and right subtrees
        self.mirror(node.left)
        self.mirror(node.right)

Time Complexity

• Recursively Traversing the Binary Tree:

  The algorithm visits each node of the binary tree exactly once to swap its left and right children. Let n be the number of nodes in the binary tree. Since each node is processed once, the time complexity of the function is \(O(n)\).

• Swapping Nodes:

  The swap operation of the left and right child nodes is an \(O(1)\) operation for each node. Given that the algorithm performs this operation for all nodes, it does not add additional complexity beyond the traversal, so the overall time complexity remains \(O(n)\).

• Overall Time Complexity:

  The overall time complexity is \(O(n)\), where n is the number of nodes in the binary tree.

Space Complexity

• Recursive Call Stack:

  The space complexity is determined by the recursion stack. In the worst case, the height of the binary tree could be n (in the case of a skewed tree), leading to an \(O(n)\) space complexity. For a balanced binary tree, the height would be \(O(\log n)\), making the space complexity \(O(\log n)\).

• Space for Variables:

  The algorithm uses a single temporary pointer temp to swap nodes, which requires \(O(1)\) space.

• Overall Space Complexity:

  The overall space complexity is \(O(h)\), where h is the height of the tree. In the worst case, it is \(O(n)\); in the average case of a balanced tree, it is \(O(\log n)\).