N-Queen Problem

The n-queens puzzle is the problem of placing n queens on a (n×n) chessboard such that no two queens can attack each other.
Given an integer n, find all distinct solutions to the n-queens puzzle. Each solution contains distinct board configurations of the n-queens placement, where the solutions are a permutation of [1,2,3..n] in increasing order, here the number in the ith place denotes that the ith-column queen is placed in the row with that number. For eg below figure represents a chessboard [3 1 4 2].

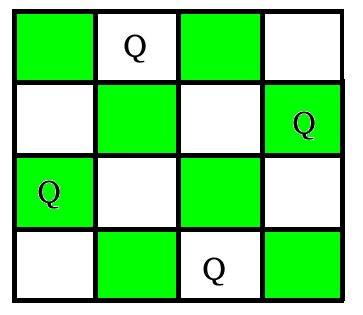
Examples:

Input: 1
Output: [1]
Explaination: Only one queen can be placed in the single cell available.

Input: 4
Output: [[2 4 1 3 ],[3 1 4 2 ]]
Explaination: These are the 2 possible solutions.

Expected Time Complexity: O(n!)
Expected Auxiliary Space: O(n²) 

Constraints:
1 ≤ n ≤ 10

Approach 01:

class Solution {
public:
    vector<bool> columns;  // Tracks used columns
    vector<bool> leftDiagonals;  // Tracks used left diagonals
    vector<bool> rightDiagonals;  // Tracks used right diagonals

    // Helper function to find all possible solutions for placing queens
    void solveNQueens(int n, vector<vector<int>>& solutions, vector<int>& currentSolution, int row) {
        if (row == n) {  // If all queens are placed
            solutions.push_back(currentSolution);
            return;
        }

        for (int col = 0; col < n; col++) {
            if (!columns[col] && !leftDiagonals[n + col - row - 1] && !rightDiagonals[row + col]) {
                currentSolution.push_back(col + 1);
                columns[col] = leftDiagonals[n + col - row - 1] = rightDiagonals[row + col] = true;
                
                solveNQueens(n, solutions, currentSolution, row + 1);
                
                // Backtrack
                columns[col] = leftDiagonals[n + col - row - 1] = rightDiagonals[row + col] = false;
                currentSolution.pop_back();
            }
        }
    }

    vector<vector<int>> nQueen(int n) {
        vector<vector<int>> solutions;
        vector<int> currentSolution;

        // Initialize vectors to track columns and diagonals
        leftDiagonals = vector<bool>(2 * n - 1);
        rightDiagonals = vector<bool>(2 * n - 1);
        columns = vector<bool>(n);

        solveNQueens(n, solutions, currentSolution, 0);
        return solutions;
    }
};

class Solution:
    def __init__(self):
        self.columns = []  # Tracks used columns
        self.leftDiagonals = []  # Tracks used left diagonals
        self.rightDiagonals = []  # Tracks used right diagonals

    # Helper function to find all possible solutions for placing queens
    def solveNQueens(self, n, row, currentSolution, solutions):
        if row == n:  # If all queens are placed
            solutions.append(currentSolution.copy())
            return

        for col in range(n):
            if (not self.columns[col] and
                not self.leftDiagonals[n + col - row - 1] and
                not self.rightDiagonals[row + col]):

                # Place the queen
                currentSolution.append(col + 1)
                self.columns[col] = self.leftDiagonals[n + col - row - 1] = self.rightDiagonals[row + col] = True

                # Recurse to the next row
                self.solveNQueens(n, row + 1, currentSolution, solutions)

                # Backtrack
                self.columns[col] = self.leftDiagonals[n + col - row - 1] = self.rightDiagonals[row + col] = False
                currentSolution.pop()

    def nQueen(self, n):
        solutions = []
        currentSolution = []

        # Initialize lists to track columns and diagonals
        self.leftDiagonals = [False] * (2 * n - 1)
        self.rightDiagonals = [False] * (2 * n - 1)
        self.columns = [False] * n

        # Start the recursive process
        self.solveNQueens(n, 0, currentSolution, solutions)
        return solutions

Time Complexity

• Recursive Backtracking:

  The recursive backtracking algorithm explores all possible placements of queens on the board. In the worst case, the time complexity is \( O(n!) \), where \( n \) is the number of queens (or the size of the board). This is because the algorithm attempts to place a queen in each column of every row, and for each valid placement, it recurses to place the next queen.

• Checking Constraints:

  For each placement, the algorithm checks if the column and diagonals are free using the columns, leftDiagonals, and rightDiagonals vectors. These checks are done in constant time, so they do not affect the overall time complexity of \( O(n!) \).

• Overall Time Complexity:

  The overall time complexity is \( O(n!) \), dominated by the recursive backtracking approach.

Space Complexity

• Column and Diagonal Tracking:

  The vectors columns, leftDiagonals, and rightDiagonals require \( O(n) \), \( O(2n – 1) \), and \( O(2n – 1) \) space, respectively, for tracking which columns and diagonals are occupied. This results in a total space complexity of \( O(n) \) for the tracking arrays since all are linear in size relative to \( n \).

• Recursive Call Stack:

  The depth of the recursive call stack can go up to \( n \), corresponding to the number of rows. This results in an additional space complexity of \( O(n) \) for the call stack.

• Storage for Solutions:

  In the worst case, there can be up to \( O(n!) \) solutions, and each solution requires \( O(n) \) space to store the positions of the queens. Thus, the total space complexity for storing the solutions can be \( O(n \cdot n!) \).

• Overall Space Complexity:

  The overall space complexity is \( O(n \cdot n!) \), primarily due to the storage required for all potential solutions.