Given a singly linked list’s head. Your task is to complete the function alternatingSplitList() that splits the given linked list into two smaller lists. The sublists should be made from alternating elements from the original list.
Note:
- The sublist should be in the order with respect to the original list.
- Yourhave to return an array containing the both sub-linked lists.
Examples:
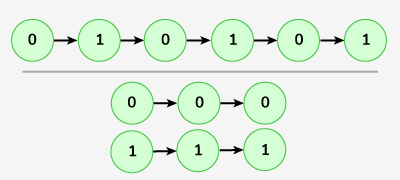
Input: LinkedList = 0->1->0->1->0->1
Output: 0->0->0 , 1->1->1
Explanation: After forming two sublists of the given list as required, we have two lists as: 0->0->0 and 1->1->1.
Input: LinkedList = 2->5->8->9->6
Output: 2->8->6 , 5->9
Explanation: After forming two sublists of the given list as required, we have two lists as: 2->8->6 and 5->9.
Input: LinkedList: 7
Output: 7 , <empty linked list>
Constraints:
1 <= number of nodes <= 100
1 <= node -> data <= 104
Approach 01:
-
C++
-
Python
class Solution {
public:
// Function to split a linked list into two lists alternately
vector<Node*> alternatingSplitList(struct Node* head) {
Node* list01 = nullptr; // Head of the first alternating list
Node* list02 = nullptr; // Head of the second alternating list
Node* list01Tail = nullptr; // Tail of the first alternating list
Node* list02Tail = nullptr; // Tail of the second alternating list
int counter = 0; // Alternating counter
while (head != nullptr) {
if (counter % 2 == 0) {
// Add the current node to list01
if (list01 == nullptr) {
list01 = head;
list01Tail = list01;
} else {
list01Tail->next = head;
list01Tail = list01Tail->next;
}
} else {
// Add the current node to list02
if (list02 == nullptr) {
list02 = head;
list02Tail = list02;
} else {
list02Tail->next = head;
list02Tail = list02Tail->next;
}
}
head = head->next;
counter++;
}
// Ensure the lists are properly terminated
if (list01Tail != nullptr)
list01Tail->next = nullptr;
if (list02Tail != nullptr)
list02Tail->next = nullptr;
// Return both lists as a vector
return {list01, list02};
}
};
class Solution:
def alternatingSplitList(self, head):
list01 = None # Head of the first alternating list
list02 = None # Head of the second alternating list
list01Tail = None # Tail of the first alternating list
list02Tail = None # Tail of the second alternating list
counter = 0 # Alternating counter
while head is not None:
if counter % 2 == 0:
# Add the current node to list01
if list01 is None:
list01 = head
list01Tail = list01
else:
list01Tail.next = head
list01Tail = list01Tail.next
else:
# Add the current node to list02
if list02 is None:
list02 = head
list02Tail = list02
else:
list02Tail.next = head
list02Tail = list02Tail.next
head = head.next
counter += 1
# Ensure the lists are properly terminated
if list01Tail is not None:
list01Tail.next = None
if list02Tail is not None:
list02Tail.next = None
# Return both lists as a tuple
return list01, list02
Time Complexity
- Traversal of the Linked List:
The function processes each node in the linked list exactly once. Since it traverses through all the nodes of the original linked list in a single loop, the time complexity is proportional to the number of nodes in the list, denoted by \(n\).
- Operations per Node:
Each node is either added to
list01orlist02. These operations involve pointer manipulation, which takes constant time \(O(1)\) per node. - Overall Time Complexity:
The overall time complexity is \(O(n)\), where
nis the total number of nodes in the linked list.
Space Complexity
- In-Place Operations:
The function modifies the original linked list in place. It does not create any new nodes but instead reuses the existing nodes and adjusts their
nextpointers. - Auxiliary Variables:
The function uses a constant number of pointers (e.g.,
list01Tail,list02Tail, andcounter), which require constant space \(O(1)\). - Returned Vector:
The function returns a vector of two pointers, which also takes constant space \(O(1)\).
- Overall Space Complexity:
The overall space complexity is \(O(1)\), as no additional space is used proportional to the input size.