Stock Buy and Sell – Multiple Transaction Allowed

The cost of stock on each day is given in an array price[]. Each day you may decide to either buy or sell the stock at price[i], you can even buy and sell the stock on the same day. Find the maximum profit that you can get.

Note: A stock can only be sold if it has been bought previously and multiple stocks cannot be held on any given day.

Examples:

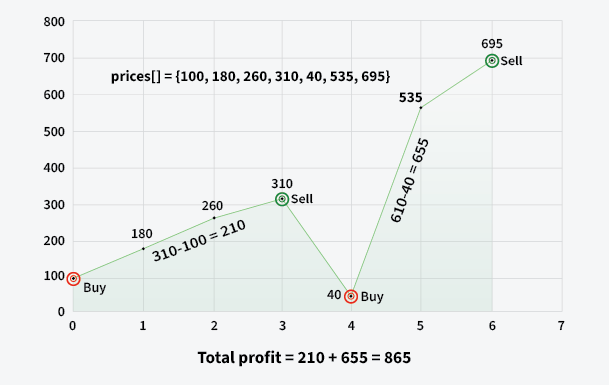
Input: prices[] = [100, 180, 260, 310, 40, 535, 695]
Output: 865
Explanation: Buy the stock on day 0 and sell it on day 3 => 310 – 100 = 210. Buy the stock on day 4 and sell it on day 6 => 695 – 40 = 655. Maximum Profit = 210 + 655 = 865.

Input: prices[] = [4, 2, 2, 2, 4]
Output: 2
Explanation: Buy the stock on day 3 and sell it on day 4 => 4 – 2 = 2. Maximum Profit = 2.

Constraints:
1 <= prices.size() <= 10⁵
0 <= prices[i] <= 10⁴

Approach 01:

#include <vector>
using namespace std;

class Solution {
 public:
  int maximumProfit(vector<int>& stockPrices) {
    int totalProfit = 0;

    for (int day = 1; day < stockPrices.size(); ++day) {
      if (stockPrices[day - 1] < stockPrices[day]) {
        totalProfit += stockPrices[day] - stockPrices[day - 1];
      }
    }

    return totalProfit;
  }
};

from typing import List

class Solution:
    def maximumProfit(self, stockPrices: List[int]) -> int:
        totalProfit = 0

        for day in range(1, len(stockPrices)):
            if stockPrices[day - 1] < stockPrices[day]:
                totalProfit += stockPrices[day] - stockPrices[day - 1]

        return totalProfit

Time Complexity

• Single Iteration:

  The function iterates through the stockPrices array once, comparing consecutive days. This takes \( O(n) \), where \( n \) is the size of the stockPrices array.

• Overall Time Complexity:

  The overall time complexity is \( O(n) \).

Space Complexity

• Auxiliary Variables:

  Variables like totalProfit and day use \( O(1) \) space.

• Input Array:

  The input array stockPrices is not included in the space complexity calculation as it is given as input.

• Overall Space Complexity:

  The overall space complexity is \( O(1) \).