Trapping Rain Water

Given an array arr[] with non-negative integers representing the height of blocks. If the width of each block is 1, compute how much water can be trapped between the blocks during the rainy season. 

Examples:

Input: arr[] = [3, 0, 1, 0, 4, 0 2]
Output: 10
Explanation: Total water trapped = 0 + 3 + 2 + 3 + 0 + 2 + 0 = 10 units.

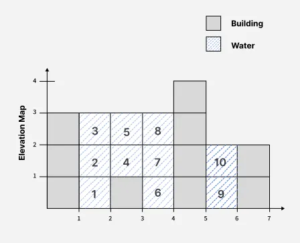
Input: arr[] = [3, 0, 2, 0, 4]
Output: 7
Explanation: Total water trapped = 0 + 3 + 1 + 3 + 0 = 7 units.

Input: arr[] = [1, 2, 3, 4]
Output: 0
Explanation: We cannot trap water as there is no height bound on both sides.

Input: arr[] = [2, 1, 5, 3, 1, 0, 4]
Output: 9
Explanation: Total water trapped = 0 + 1 + 0 + 1 + 3 + 4 + 0 = 9 units.

Constraints:
1 < arr.size() < 10⁵
0 < arr[i] < 10³

Approach 01:

#include <vector>
#include <algorithm>
using namespace std;

class Solution {
public:
    int maxWater(vector<int> &heights) {
        int totalWater = 0;         // To store the total trapped water
        int leftMax = 0, rightMax = 0; // Maximum heights from the left and right
        int leftPointer = 0, rightPointer = heights.size() - 1; // Pointers to traverse the array

        while (leftPointer < rightPointer) {
            leftMax = max(leftMax, heights[leftPointer]);   // Update left maximum
            rightMax = max(rightMax, heights[rightPointer]); // Update right maximum

            if (heights[leftPointer] <= heights[rightPointer]) {
                totalWater += leftMax - heights[leftPointer]; // Add trapped water on the left side
                leftPointer++;
            } else {
                totalWater += rightMax - heights[rightPointer]; // Add trapped water on the right side
                rightPointer--;
            }
        }

        return totalWater;
    }
};

class Solution:
    def maxWater(self, heights):
        totalWater = 0       # To store the total trapped water
        leftMax = 0          # Maximum height from the left
        rightMax = 0         # Maximum height from the right
        leftPointer = 0      # Pointer to traverse from the left
        rightPointer = len(heights) - 1  # Pointer to traverse from the right

        while leftPointer < rightPointer:
            leftMax = max(leftMax, heights[leftPointer])    # Update left maximum
            rightMax = max(rightMax, heights[rightPointer]) # Update right maximum

            if heights[leftPointer] <= heights[rightPointer]:
                totalWater += leftMax - heights[leftPointer] # Add trapped water on the left side
                leftPointer += 1
            else:
                totalWater += rightMax - heights[rightPointer] # Add trapped water on the right side
                rightPointer -= 1

        return totalWater

Time Complexity:

• Single Pass:

  The algorithm uses two pointers that traverse the array from both ends towards the center. Each element is processed at most once, resulting in \( O(n) \), where \( n \) is the size of the input array.

• Overall Time Complexity:

  \( O(n) \).

Space Complexity:

• Constant Extra Space:

  The algorithm uses a constant amount of extra space for variables like leftMax, rightMax, leftPointer, and rightPointer, regardless of the input size.

• Input Array:

  The input array is read-only and does not require additional storage.

• Overall Space Complexity:

  \( O(1) \).